Document Actions
Light in Random Media
Light interaction with random media is ubiquitous in nature and has found vast applications in applied sciences. Well-known examples for random media are biological tissue, atmosphere, ocean, and colloidal systems. The emergent light after interaction with a random medium (transillumination or backscattering) has been actively pursued as a means of non-invasively probing the internal structure of the random medium in the pasr decades (photonic diagnostics of random media). Light interaction with random media is ubiquitous in nature and has found vast applications in applied sciences. Well-known examples for random media are biological tissue, atmosphere, ocean, and colloidal systems. The emergent light after interaction with a random medium (transillumination or backscattering) has been actively pursued as a means of non-invasively probing the internal structure of the random medium in the pasr decades (photonic diagnostics of random media).
The propagation of multiply scattered light in random media follows a universal law and light diffuses after a sufficient number of scattering events has occured. Light diffusion is characterized by one length scale - the transport mean free path, lt, i.e., the distance over which the initial light propagation direction is randomized. By treating analytically the propagation of polarized light in turbid media as a random walk of vector photons, I have identified two additional length scales governing depolarization of the multiply scattering polarized light: (1) the characteristic length, lp, for polarized light to become isotropic in its linear polarization and propagation directions [1, 2], and (2) the characteristic length, lx, for circular polarized light to lose its helicity [3]. This also leads to a simple analysical model for the circular polarization memory effect of light. Other highlights of my relevant past work include a cumulant transport model for radiative transfer, providing a much more accurate transport model than the commonly used diffusion approximation [4, 5, 6]; an Electric Field Monte Carlo method (EMC) to simulate propagation, decoherence and depolarization of polarized light in random media; and low coherence enhanced backscattering of light [7, 8].
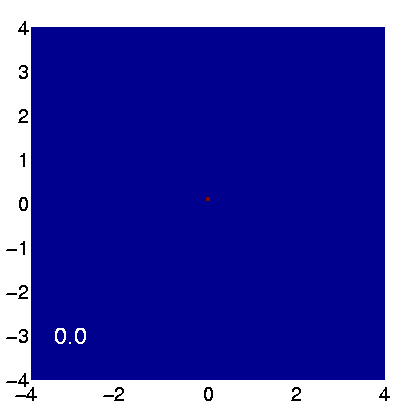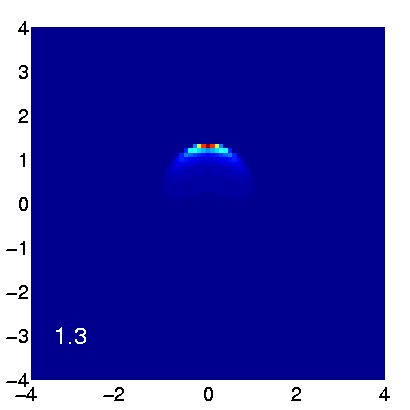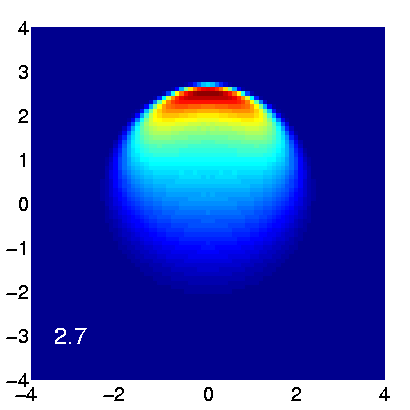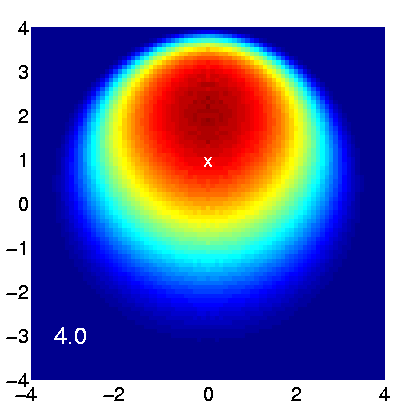
Figure 1: Propagation of a collimated beam in random media. The x,y coordinates are measured in, lt, the transport mean free path.
On-going research projects:
- Unification of light depolarization and decoherence into the model describing light propagation in random media. This work shall explore wave-shaping in the control of light propagation in turbid media and address the important practical problem where light is used to interrogate small turbid volumes or subsurface.
Selected Publications
[1] M. Xu, W. Cai, M. Lax, and R. R. Alfano. Stochastic view of photon migration in turbid media. arXiv:cond-mat/0401409, 2004.
[2] M. Xu and R. R. Alfano. Random walk of polarized light in turbid media. Phys. Rev. Lett., 95:213905, 2005.
[3] M. Xu and R. R. Alfano. Circular polarization memory of light. Phys. Rev. E, 72:065601(R), 2005.
[4] M. Xu, W. Cai, M. Lax, and R. R. Alfano. A photon transport forward model for imaging in turbid media. Opt. Lett., 26(14):1066-1068, 2001.
[5] M. Xu, W. Cai, M. Lax, and R. R. Alfano. Photon migration in turbid media using a cumulant approximation to radiative transfer. Phys. Rev. E, 65:066609, 2002.
[6] W. Cai, M. Xu, and R. R. Alfano. Analytical form of the particle distribution based on the cumulant solution of the elastic Boltzmann transport equation. Phys. Rev. E, 71:041202, 2005. (10 pages).
[7] Min Xu. Low coherence enhanced backscattering beyond diffusion. Opt. Lett., 33:1246-1248, 2008.
[8] Xiuwei Zhu, Luyao Lu, Zili Cao, Bixin Zeng, and Min Xu. Transmission matrix-based Electric field Monte Carlo study and experimental validation of the propagation characteristics of Bessel beams in turbid media. Opt. Lett., 43(19):4835, oct 2018.

