Quantitative modeling of tissue scattering and absorption properties is fundamental to determine light transport and energy deposition in tissue, key to both diagnostic and therapeutic applications of light. The rich spectroscopic behavior of biological tissue arising from its complex structure, as one main strength of optical interaction with biological tissue and cells compared to other biomedical imaging modalities, has also provided a powerful noninvasive probe to structural alterations in tissue due to disease or physiology. It is hence critical to establish connection between the characteristics of light scattering to the complex structure of tissue and cells.

A fractal continuous random medium model [1, 2, 3] has been proposed for light scattering by biological medium based on the observation that many biological tissues have fractal-like organization and on a macroscopic scale the constituents of tissue have no clear boundaries and merge into a quasi-continuum structure. The model has been shown to describe well light scattering by both tissue and cell suspensions. Via a unified Mie and fractal model derived from the superposition rule for light scattering by a composite particle [4], the fractal dimension and the correlation length reflecting both the morphological structure of tissue and the nuclear structure can be detected by spectroscopic light scattering measurement [3, 5]. The unified model is currently the only analatical model for light scattering by cells that describes correctly both the Mie resonance structure near forward scattering direction and the fractal scattering at larger angles. Preliminary experimental results show the fractal model can be successfully applied to discriminate accurately normal and malignant prostate tissues [6].

Figure 1: Experimental (solid circles) and unified model fitting (solid line) results for the scattering spectra of the SiHa cell suspension at 10 representative scattering angles. The size distributions for the cell and the nucleus were measured separately by microscopy and not fitted. Note the Mie resonance at small scattering angles and the fractal scatering behavior at larger angles.

A novel statistical theory of light extinction by soft particles [7, 8] has been developed and successfully applied to characterize bacteria and other soft particles of arbitrary shapes and sizes in vivo [9, 10]. For example, both refractive index and size change of Bacillus subtilis endospores during heat-shock-induced activation have been monitored in situ [10]. This technique has applications in biosensing of bacterias. Light scattering by fractal aggregates has also been studied to monitor the aggregation of clays [11].

The latest line of research is to characterize the superficial layer of tissue where approximately 90% of cancer initiates using low coherence enhanced backscattering of light [12, 13]. Enhanced backscattering is one fascinating physical phenomenon (also known as weak localization) of multiple scattering light that originates from the constructive interference between the light waves propagating along a pair of time-reversal trajectories. Low spatial coherence of incident light ensures interference only occurs for light remitting within the coherence length away from the incident point and hence limits the penetration depth of low coherence enhanced backscattering light. The preliminary results show that the low coherence enhanced backscattering spectrum can be used to extract both the dominant scatterer size and the fractal dimension of the medium. Being able to probe the nuclear structural change noninvasively at subsurface is significant and finds numerous applications in cancer screening and diagnostics.

Plum pudding random medium model for biological tissue 

Variations in the refractive index cause tissue to scatter light. Light of longer wavelength is expected to be more isotropically scattered into all directions as the scatterers appear smaller with respect to the wavelength and the anisotropy factor (g) defined as the mean cosine of the scattering angles gets smaller. This widely-accepted wavelength dependence of g is, however, contradictory to that found by thorough measurements within visible and near-infrared spectral range. The "anomalous" increase of g with the probing wavelength seems to be the rule rather than the exception for tissue light scattering. The anisotropy factor is one central parameter in photon multiple scattering and migration that bears the direct relation to the morphology and optical properties of the underlying microscopic scattering constituents. This contradiction between experiments and theory on g, in particular, reveals the current lack in the understanding of the nature of tissue light scattering.

We have developed, for the first time, a plum pudding random medium (PPRM) model [14] for biological tissue. PPRM properly describes tissue as a continuum of background refractive index fluctuation (pudding) yet with some prominent structures (plum) which are distinctive from the background medium. In this unified view, tissue light scattering is a superposition of both plums and pudding [4, 3]. The former includes, for example, the nuclear structure in soft tissue and fiber bundles in muscle. The latter incorporates smaller scattering structures such as organelles and refractive index variations throughout the tissue continuum. The powerlaw dependence of the reduced scattering coefficient is attributed to the fractal scattering pudding [1] whereas the distinctive prominent structure is responsible for the observed "anomalous" anisotropy trend. PPRM provides a potential resolution to the long-lasting puzzle in the spectroscopic properties of tissue.

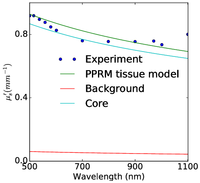
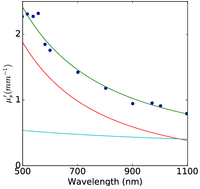
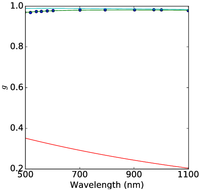
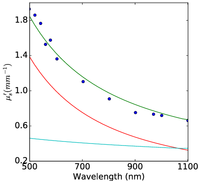
Figure 2: Plum pudding random medium tissue model fitting to from top row to bottom row (a) normal breast adipose tissue, (b) normal glandular breast tissue, (c) fibrocystic tissue, (d) fibroadenoma, and (e) ductal carcinoma. The columns from left to right show the scattering coefficient μ_s, the reduced scattering coefficient μ_s′, and the anisotropy factor g. The background refractive index fluctuation and the core are shown together with the PPRM tissue model. Experimental data is adapted from Peters et al, Phys. Med. Biol., 35(9):1317-1334, 1990.

In vivo optical histopathology of deep tissue has long been one coveted goal of biophotonics. PPRM not only offers an analytical platform to understand and interpret light scattering by the complex structures in tissue but also have opened up a novel venue of quantifying the tissue architecture and microscopic structures from macroscopic probing of the bulk with scattered light alone. The determination of the background refractive index fluctuation and the properties of the plums completely characterizes and can further depict the tissue architecture and microscopic structure on average. PPRM may establish the foundation towards achieving such extremely desirable remote microscopy of biological tissue derived from non-contact spectroscopic light scattering measurement without tissue excision. This potential was demonstrated by visualizing the fine microscopic structural alterations in breast tissue (adipose, glandular, fibrocystic, fibroadenoma, and ductal carcinoma) deduced from noncontact spectroscopic measurement alone.

(a)  (b)

(c)

(d)  (e)

Figure 3: The plum and pudding (background refractive index fluctuation) in (a) normal breast adipose tissue, (b) normal glandular breast tissue, (c) fibrocystic tissue, (d) fibroadenoma, and (e) ductal carcinoma derived from scattering spectroscopy measurement. The whole window size is 30μm × 30μm. The blue square delineates a unit cell which contains exactly one core. A core of most probable radius is shown, surrounded by a shaded area of radius at which the number density of the core drops to half maximum.

On-going research projects:

• Deep tissue histopathology without tissue excision (remote microscopy) from spectroscopic light scattering based on the plum pudding random model of biological tissue

Selected Publications

[1]   M. Xu and R. R. Alfano. Fractal mechanisms of light scattering in biological tissue and cells. Opt. Lett., 30:3051-3053, 2005.

[2]   Tao T. Wu, Jianan Y. Qu, and Min Xu. Unified Mie and fractal scattering by biological cells and subcellular structures. Opt. Lett., 32:2324-2326, 2007.

[3]   M. Xu, Tao T. Wu, and Jianan Y. Qu. Unified Mie and fractal scattering by cells and experimental study on application in optical characterization of cellular and subcellular structures. J. Biomed. Opt., 13:038802, 2008.

[4]   M. Xu. Superposition rule for light scattering by a composite particle. Opt. Lett., 31:3223-3225, 2006.

[5]   Min Xu. Quantifying microarchitectural and light scattering differences between tumorigenic and non-tumorigenic cell models of tissue: analysis with unified Mie and fractal model. In Biomedical Optics/Digital Holography and Three-Dimensional Imaging/Laser Applications to Chemical, Security and Environmental Analysis on CD-ROM, page BTuF11, Optical Society of America, Washington, DC, 2008.

[6]   Yang Pu, Wubao Wang, Mohammad AL-Rubaiee, Swapan Kumar Gayen, and Min Xu. Determination of optical coefficients and fractal dimensional parameters of cancerous and normal prostate tissues. Appl. Spectroscopy, 66:828-834, 2012.

[7]   M. Xu, M. Lax, and R. R. Alfano. Light anomalous diffraction using geometrical path statistics of rays and gaussian ray approximation. Opt. Lett, 28:179-181, 2003.

[8]   M. Xu and A. Katz. Light Scattering Reviews, volume III, chapter Statistical Interpretation of Light Anomalous Diffraction by Small Particles and its Applications in Bio-agent Detection and Monitoring, pages 27-68. Springer, 2008.

[9]   A. Katz, A. Alimova, M. Xu, E. Rudolph, M. Shah, H. Savage, R. Rosen, S. A. McCormick, and R. R. Alfano. Bacteria size determination by elastic light scattering. IEEE JSTQE, 9:277-287, 2003.

[10]   A. Katz, Alexandra Alimova, M. Xu, Paul Gottlieb, Elizabeth Rudolph, J. C. Steiner, and R. R. Alfano. In Situ determination of refractive index and size of Bacillus spores by light extinction. Opt. Lett., 30:589-591, 2005.

[11]   Alexandra Alimova, A. Katz, Julian Orozco, Hui Wei, Paul Gottlieb, Elizabeth Rudolph, J. C. Steiner, and Min Xu. Broadband light scattering measurements of the time evolution of the fractal dimension of smectite clay aggregates. J. Opt. A, 11:105706, 2009. (Feature Article).

[12]   Min Xu. Low coherence enhanced backscattering beyond diffusion. Opt. Lett., 33:1246-1248, 2008.

[13]   Min Xu. Coherent backscattering of polarized light for tissue diagnostics: an electric field Monte Carlo study. In Steven L. Jacques, William P. Roach, and Robert J. Thomas, editors, Optical Interactions with Tissue and Cells XVIIII, 6854, page 68541A, 2008.

[14]   Min Xu. Plum pudding random medium model of biological tissue toward remote microscopy from spectroscopic light scattering. Biomed. Opt. Express, 8:2879-2895, 2017.